Mc-Callova plošná standardizace: Porovnání verzí

Verze z 24. 4. 2016, 19:38

McCallova plošná standardizace

McCallova plošná standardizace je metoda, která se používá k transformaci rozdělení s vysokou šikmostí (nesymetrické rozdělení) na normální rozdělení. Pomocí této metody linearizujeme jinak nelineární vztahy nebo upravujeme tvar rozdělení dat tak, aby se více podobalo rozdělení popsanému Gaussovou křivkou. Jde o transformaci hrubých skórů na normální distribuci transformovaných standardních skórů. Podle axiomu normality totiž předpokládáme, že duševní vlastnosti mají (podobně jako fyzické) v populaci normální rozložení. Předpokládá se tedy, že nerovnoměrné rozložení výsledků je dané spíše charakteristikami testu.

Postup:

Vytvoříme sloupec hrubých skórů (HS), od nejnižšího dosažitelného skóru po nejvyšší
K HS přiřadíme absolutní četnost (např. 6 lidí získalo v testu 12 bodů ->k HS 12 přiřadíme absolutní četnost 6)
V dalším sloupci vyjádříme relativní četnost (absolutní četnost vydělíme N, to je např. počet lidí, kterým byl test zadán)
Vypočítáme kumulativní relativní četnost (sčítáme relativní četnosti, musí končit hodnotou 1!)
U diskrétních dat korigujeme na spojitost (k předchozí kumulativní relativní četnosti připočítáváme vždy jen polovinu relativní četnosti)
Vyčíslíme Z-skór (v Excelu pomocí funkce NORMSINV z = (X - μ) / σ)
Na základě Z-skóru můžeme převést na libovolný další standardní skór (př. steny, IQ-skór)

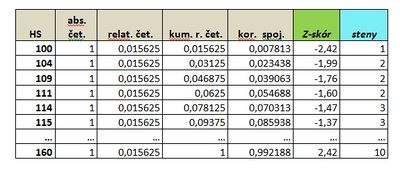
Ukázka postupu:

@@ Řádek 5: / Řádek 5: @@
 '''Postup:'''
-) Vytvoříme sloupec hrubých skórů (HS), od nejnižšího dosažitelného skóru po nejvyšší.
+# Vytvoříme sloupec hrubých skórů (HS), od nejnižšího dosažitelného skóru po nejvyšší
+# K HS přiřadíme absolutní četnost (např. 6 lidí získalo v testu 12 bodů ->k HS 12 přiřadíme absolutní četnost 6)
-) K HS přiřadíme absolutní četnost (např. 6 lidí získalo v testu 12 bodů ->k HS 12 přiřadíme absolutní četnost 6).
+# V dalším sloupci vyjádříme relativní četnost (absolutní četnost vydělíme N, to je např. počet lidí, kterým byl test zadán)
+# Vypočítáme kumulativní relativní četnost (sčítáme relativní četnosti, musí končit hodnotou 1!)
-) V dalším sloupci vyjádříme relativní četnost (absolutní četnost vydělíme N, to je např. počet lidí, kterým byl test zadán)
+# U diskrétních dat korigujeme na spojitost (k předchozí kumulativní relativní četnosti připočítáváme vždy jen polovinu relativní četnosti)
+# Vyčíslíme Z-skór (v Excelu pomocí funkce NORMSINV ''z = (X - μ) / σ'')
-) Vypočítáme kumulativní relativní četnost (sčítáme relativní četnosti, musí končit hodnotou 1!).
+# Na základě Z-skóru můžeme převést na libovolný další standardní skór (př. steny, IQ-skór)
-) U diskrétních dat korigujeme na spojitost (připočítáváme vždy jen polovinu relativní četnosti).
-) Vyčíslíme Z-skór
-• v Excelu pomocí funkce NORMSINV
-• z = (X - μ) / σ
-) Na základě Z-skóru můžeme převést na libovolný další standardní skór (př. steny, IQ-skór)
 [[File:tabulka1.jpg|400px]]