Normální rozdělení: Porovnání verzí
(Normální rozdělení) |
|||
| (Není zobrazena jedna mezilehlá verze od stejného uživatele.) | |||
| Řádek 12: | Řádek 12: | ||
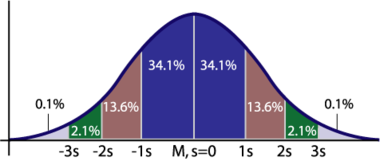
* Vždy můžeme vypočítat procento případů spadajících do určitého intervalu kolem průměru. Do jedné směrodatné odchylky (σ) na každou stranu spadá 68,26% případů. Do dvou směrodatných odchylek (2σ) na každou stranu spadá 95,34% případů. Jinak řečeno je 95% pravděpodobnost, že náhodně vybraný případ bude ležet v intervalu ±2σ kolem průměru (přesně je to do ±1,96σ). Do ±3σ spadne přesně 99,7% případů (''viz obrázek'').<ref name="analyza" /> | * Vždy můžeme vypočítat procento případů spadajících do určitého intervalu kolem průměru. Do jedné směrodatné odchylky (σ) na každou stranu spadá 68,26% případů. Do dvou směrodatných odchylek (2σ) na každou stranu spadá 95,34% případů. Jinak řečeno je 95% pravděpodobnost, že náhodně vybraný případ bude ležet v intervalu ±2σ kolem průměru (přesně je to do ±1,96σ). Do ±3σ spadne přesně 99,7% případů (''viz obrázek'').<ref name="analyza" /> | ||
| − | == Zjišťování normálního rozdělení == | + | == Zjišťování normálního rozdělení v SPSS == |
| − | + | * '''Histogram''' (grafické prozkoumání rozložení četností výběrového souboru) | |
| − | + | Analyze - Descriptive statistics - Frequencies - Charts - Histograms + with normal curve | |
| − | + | ||
| − | + | * '''P-P graf''' (''probability to probability plot, P-P plot'') | |
| + | Analyze - Descriptive statistics - P-P Plots | ||
| + | |||
| + | * Otestování '''symetričnosti rozdělení''' pomocí [[Šikmost a špičatost|šikmosti]] (''skewness'') a [[Šikmost a špičatost|špičatosti]] (''kurtosis'') | ||
| + | Descriptive Statistics - Frequencies - Statistics + zakliknout Skewness a Kurtosis | ||
| + | |||
| + | * '''Kolmogorův-Smirnovův test''' (K-S test), který statisticky hodnotí, jestli je rozdíl mezi pozorovaným rozdělením a teoretickým normálním rozdělením natolik malý, že jej můžeme připsat náhodě (výběrové chybě). Nultá hypotéza tedy zní, že se pozorované rozdělení od normálního neliší, a proto statisticky významný nález ukazuje na jiné než normální rozložení proměnné. Výsledkem v SPSS bude několik tabulek, tabulka s názvem ''Tests of Normality'' označuje Kolmogorův-Smirnovův test.<ref name="analyza" /> | ||
| + | Analyze - Descriptive Statistics - Explore - Plots + zaškrtnout Normality plots with tests + odškrtnout Stem-and-leaf | ||
Pokud rozdělení normální není, použijeme k dalším analýzám [[Statistické neparametrické testy|neparametrické testy]] (nebo transformujeme distribuci proměnné).<ref name="analyza" /> | Pokud rozdělení normální není, použijeme k dalším analýzám [[Statistické neparametrické testy|neparametrické testy]] (nebo transformujeme distribuci proměnné).<ref name="analyza" /> | ||
Aktuální verze z 1. 6. 2016, 13:41
Normální rozdělení (Gaussova křivka) pravděpodobnosti je jedno z nejpoužívanějších rozložení četností výskytu určitého jevu. Má známý zvoncovitý tvar a je typické pro řadu biologických, psychických i sociálních jevů a vlastností. "Normální" v názvu tohoto rozdělení znamená "řídící se zákonem, předpisem nebo modelem". Podle francouzského statistika Adolpha Quételeta (1796-1874) normální rozdělení není nic jiného, než že se příroda snaží vytvořit ideální typ (reprezentovaný průměrem), avšak v různé míře chybuje.[1]
Normální rozdělení je jako každé jiné statistické rozdělení především myšlenkovým modelem a matematickým ideálem. Je to však model vylice významný. Prakticky vždy se zajímáme, jestli se naše naměřené hodnoty podobají normálnímu rozložení. Pokud ano, můžeme využít řadu statistických testů, které jsou na předpokladu normálního rozložení založeny (nazývají se parametrické).[1]
Obsah
Důležitost pro statistiku
Pro statické zpracování dat je normální rozdělení důležité díky následujícím charakteristikám:
- Rozdělení je symetrické a většina hodnot se soustředí kolem průměru. Polovina hodnot je větší než průměr a polovina menší.
- Aritmetický průměr je současně mediánem a modem (jako nejčastěji se vyskytující hodnota).
- Normální rozdělení je jednomodální (má jeden vrchol)
- Vždy můžeme vypočítat procento případů spadajících do určitého intervalu kolem průměru. Do jedné směrodatné odchylky (σ) na každou stranu spadá 68,26% případů. Do dvou směrodatných odchylek (2σ) na každou stranu spadá 95,34% případů. Jinak řečeno je 95% pravděpodobnost, že náhodně vybraný případ bude ležet v intervalu ±2σ kolem průměru (přesně je to do ±1,96σ). Do ±3σ spadne přesně 99,7% případů (viz obrázek).[1]
Zjišťování normálního rozdělení v SPSS
- Histogram (grafické prozkoumání rozložení četností výběrového souboru)
Analyze - Descriptive statistics - Frequencies - Charts - Histograms + with normal curve
- P-P graf (probability to probability plot, P-P plot)
Analyze - Descriptive statistics - P-P Plots
- Otestování symetričnosti rozdělení pomocí šikmosti (skewness) a špičatosti (kurtosis)
Descriptive Statistics - Frequencies - Statistics + zakliknout Skewness a Kurtosis
- Kolmogorův-Smirnovův test (K-S test), který statisticky hodnotí, jestli je rozdíl mezi pozorovaným rozdělením a teoretickým normálním rozdělením natolik malý, že jej můžeme připsat náhodě (výběrové chybě). Nultá hypotéza tedy zní, že se pozorované rozdělení od normálního neliší, a proto statisticky významný nález ukazuje na jiné než normální rozložení proměnné. Výsledkem v SPSS bude několik tabulek, tabulka s názvem Tests of Normality označuje Kolmogorův-Smirnovův test.[1]
Analyze - Descriptive Statistics - Explore - Plots + zaškrtnout Normality plots with tests + odškrtnout Stem-and-leaf
Pokud rozdělení normální není, použijeme k dalším analýzám neparametrické testy (nebo transformujeme distribuci proměnné).[1]
Odkazy
Reference
Použitá literatura
- Mareš, P., Rabušic, L., Soukup, P. (2015). Analýza sociálněvědních dat (nejen) v SPSS. 1. vyd. Brno: Masarykova univerzita. ISBN 978-80-210-6362-4
Externí odkazy
- Testing Distributions for Normality - SPSS (Youtube video)
- Normality test using SPSS: How to check whether data are normally distributed (Youtube video)
- The Normal Distribution and the 68-95-99.7 Rule (Youtube video)
Související články
- Statistické standardní skóry
- Šikmost a špičatost
- Binomické rozdělení
- Otázky ze statistiky (NMgr Psychologie FF UK)
- Centrální limitní věta
Klíčová slova
Gaussovo rozdělení, Gaussova křivka, normální rozdělení, centrální limitní věta